Lab 04
Feedback form (Please fill this form, to give feedback about this lab)
Here is a pdf version of the ppt I covered during the lab. And the codes that I (skimmed through) / (demonstrated live).
content.pdf (The pdf version of the ppt shown)
STLPriorityQueue.cpp (The STL Priority Queue implementation)
UVa 1203.cpp (The solution code for the problem Uva 1203 discussed in the lab which involves the use of Priority Queue)
Challenge Questions -
Q) For PS2 D, try to code your priority queue using pointers instead of using an array based approach.
Solution
Refer to the AVL implementation of the prof and try to modify it :)Q) Given an array of N integers, find the Kth smallest element in time complexity O(N + KlogN) ?
(Note - Sorting will not work)
(Note - We do not want a randomised solution, so do not think along the lines of n_th element function in the C++ library)
Solution
Make your own min binary heap / priority queue using the demo code shown in Lab05in O(N). Then pop the first K - 1 elements and print the top obtained after the pops in O(KlogN). So total is O(N + KlogN).
But how do you make the heap in O(N) ?
You would need to build the heap in O(N), which is done by inserting the elements in a weird fashion.
Step 1 - Take the unsorted array and put them into the binary heap in any arbitrary order.
Step 2 - Do for(i = heapSize; i >= 1; i--) shiftDown(i);
i.e Basically do shiftDown for the deepest node, then 2nd deepst and so on, untill you hit the root.
Step 3 - The heap is now a valid heap you are done.
Explanation -
The step 2 is the essence of the build. First let us make this claim -
Claim 1 -
Given a subtree of heap with the root of the subtree as node "a" and it has two children, left child named as "b", right child named as "c". Let val[a], val[b], val[c] denote the values at the indices a, b and c respectively.Then if b and c are valid subtree heaps, i.e within the subtrees of "b" and "c" the properties of heap are satified. Then this subtree of "a" will also be a valid heap, given we do a single shiftDown(a) operation.
Proof -
Case 1 - When val[a] ≤ min(val[b], val[c]) (Note we are making a min Heap)
The subtree heap of "a" is already valid, so shiftDown(a) does nothing.
Case 2 - When val[a] > min(val[b], val[c])
Arbitrarily assume, that val[b] ≤ val[c]
Then "a" will be swapped with "b" during the shiftDown(a) operation. And the shiftDown(a) operation will recursively call the same operation for shiftDown(b), but now do notice that after the swap, value[b] = value[a].
So in this scenario we are ensured that the "a" would become a valid subtree heap provided "b" becomes a valid subtree heap. This is basically solving the same problem again, but for a smaller subtree. This will true, using PMI(Principal of Mathematical Induction) on this claim.
So now, we have proven Claim 1 and understand why the heap will result to be sorted after Step 2. But what about the time complexity.
Well carefully observe, let the depth of the tree be called as "h" = log2(N), then -
The number of nodes at height h are N/2.
The number of nodes at heigh h - 1 are N/4
In general the number of nodes at height x are N/2^(h - x + 1)
Let n(x) denote the number of nodes at height x.
So we have n(x) = N / 2^(h - x + 1)
Now the sum of time complexity because of the ShiftDown due to all the nodes at height h is = n(h) * 0
We multiply with 0, because they are not moved at all, and they remain at their location when shiftDown is called for them.
Similarly , what is the sum of time complexity for all nodes at height h - 1. It is n(h - 1) * 1.
More generally let S(x) denote the sum of time complexity because of shifting down all the nodes at height x. Then
S(x) = n(x) * (h - x + 1)
So we need to find sum over S(x) from x = 1 to h.
So the net time complexity = S(1) + S(2) + ... + S(h)
= n(1) * h + n(2) * (h - 1) + ... + n(h) * 0
= 1 * h + 2 * (h - 1) + 4 * (h - 2) + ... + N/2 * 0
= 0 * N/2 + 1 * N/4 + 2 * N/8 + ... + (h - 2) * 4 + (h - 1) * 1 + h * 1 (Reversing the expression)
= (0 * N)/2 + (1 * N)/4 + (2 * N)/8 + ...
This sum is then bounded by O(N) using Taylor series. The notation of math requires is pretty extensive so I will just add this image below. You can also read this build O(N) function here at stack overflow
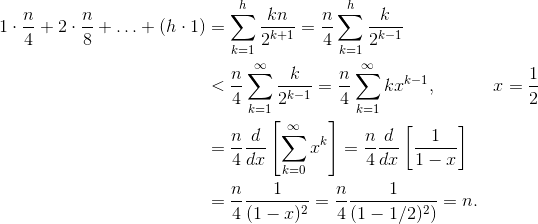
Q) We know that a Priority Queue is internally implemented using a max heap. For PS2 D, a lot of you implemented your own “max heap” and the general approach was that each node should have “2 children”. That is why it is known as “binary heap”. But let us say we make a “ternary heap”, i.e in this heap each node will have 3 children each. Then what will be the time complexity per push() and per erase() ? Would this be better than the binary heap in any aspect (time / space / … ) ?
Or you can try to calculate the time complexity for a more generic version of a “k-ary heap” where each node has “k children”.
Solution
So the shiftDown in a ternary heap is O(2 * log3(N)) and shiftUp is O(log3(N))For a more generic "k-ary heap" shiftDown is O((k - 1) * logk(N)) and shift up is O(logk(N)). Here logk(N) means log(N) with base k. Dont know why but subscript is not working on github markdown.
We can observe that shiftUp is cheaper in a k-ary heap, where k >= 2, than a binary heap, but shiftDown is more expensive.
So it would be better in scenarios where you do a lot of shiftUp and very few shiftDown. Example - There are a lot of insert operations (requiring shiftUp) and very few pop operations (requiring shiftDown). You can read more about this here (wikipedia)
Q) A kattis like question -
Given an array of N elements where all of them are initially equal to 1. You are now given Q operations where each operation is either of the 3 types -
Type 1 - Take the largest element of the array and multiply it by x, where (1 <= x <= 100000)
Type 2 - Take the largest element of the array and divide it by x, where (1 <= x <= 100000) (This division is NOT integer division, it is NORMAL division, so 5 / 2 = 2.5)
Type 3 - Print “Yes” if the (largest element of the array is > 2 * second largest element of the array). Otherwise print “No”
Assume 1 <= N <= 100000, 1 <= Q <= 100000
For Type 1 and Type 2 operations, in case of tie you are allowed to pick arbitrarily.
Also do note, that if you implement this naively in C++, you will experience overflow in int/longlong. And using Python for the bigInteger is NOT the expected solution.
Solution
I will give out the entire details sometime soon. The key idea was to use log(X) instead of X and use a binary heap aka priority queue. The idea has been ripped of from IOI Horses 2015. If you are feeling adventurous, then do give it a try. It would require knowledge of BBST / Segment Tree though.The exact solution -
Maintain a max heap and instead of putting all the values normally, put the logarithm of all the values. (You need to use the log values instead of normal ones, because normal ones would overflow if stored in an int / long long. And if you used double then their would be precision issues)
Now for type 1 operation instead of doing largest = largest * x, we will do log(largest) = log(largest * x), which is using properties of log equivalent to log(largest) = log(largest) + log(x). Do note here I am using natural log with base e, for convienience. You can do choose to use a different base.
Now for type 2, do similar thing but instead of adding log(x) just subtract log(x), because log(largest / x) is equivalent to log(largest) - log(x).
Finally for type 3, take the largest, let it be a. Pop the largest and again take the largest, i.e actually the second largest. Let it be b. Now you need to check if a > 2*b. Take log on both sides, so you need to tell if log(a) > log(2 * b) which is equal to log(a) > log(2) + log(b). This comparison can be done easily, because log(2) is simply a constant. That is it.
This was the idea of the solution in broad terms :)